Winter_leaf
관성 모멘트
관성모멘트는 직선 운동에서 질량에 대응하는 힘의 양이며, 물체가 고정된 축을 중심으로 회전운동을 지속하려는 성질의 크기를 나타낸 물리량입니다. 예를 들어 직선 운동에서 동일한 힘으로 즉 외부에서 힘이 작용하지 않는다면 질량에 의해 속도의 변화를 일으키기 어렵듯이, 같은 힘에 대해 각속도의 변화를 일으키기 어려운 정도가 관성모멘트입니다.
※ 각속도 : 회전하는 물체의 단위시간당 각위치 변화(즉, 회전하는 속도와 방향을 나타냄)
[어떤 축을 중심으로 회전하는 점질량의 관성모멘트]
I = mr2
I : 관성모멘트
m : 질량
r : 회전축으로부터 점질량까지의 거리
[일반적인 관성모멘트 공식]
기본적으로 회전하는 물체의 관성모멘트는 회전축에서 각 입자의 거리를 제곱한 다음 질량을 곱해 계산할 수 있다. 회전하는 물체를 구성하는 모든 입자에 대해 이 값을 계산하여 모두 합하면 관성모멘트를 구할 수 있다.

mi : i번째 해당하는 입자의 질량
ri : 회전축에 수직인 i번째 입자까지의 거리
위의 식은 관성모멘트를 계산하는 가장 일반적인 접근 방식이다. 하지만 물체의 모양과 회전하는 방식에 따라 적용되는 공식이 다르며, 더 정교한 대상의 경우 전체 크기를 구하기 위해 적분을 적용해야 할 수도 있다.
물체의 모양 및 회전축에 따른 관성모멘트 공식
[속이 찬 구의 관성모멘트]
구의 중심을 통과하는 축에서 회전하는 속이 찬 구

[속이 빈 얇은 구의 관성모멘트]
구의 중심을 통과하는 축에서 회전하는 얇고 무시할 수준의 벽으로 구성된 속이 빈 구

[속이 찬 원통의 관성모멘트]
원통의 중심을 통과하는 축에서 회전하는 속이 찬 원통

[일정 두께를 지닌 속이 빈 원통의 관성모멘트]
내부 반지름 R1과 외부 반지름 R2를 갖는 원통의 중심을 통과하는 축을 중심으로 회전하는 속이 빈 원통

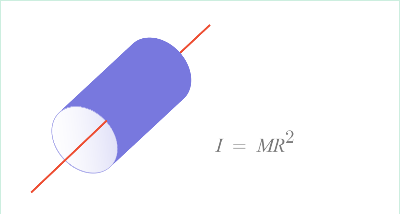
[속이 빈 얇은 원통의 관성모멘트]
원통의 중심을 통과하는 축에서 회전하는 얇고 무시할 수 있는 벽으로 구성된 속이 빈 원통
[직사각형 판의 관성모멘트]
변의 길이가 각각 a와 b인 직사각형 판의 중심에 수직인 축에서 회전하는 얇은 판

[얇은 막대의 관성모멘트]
길이가 L인 막대의 중심을 통과하는 축에서 회전하는 가느다란 막대

Winter_leaf
'1. Science' 카테고리의 다른 글
| 원소를 변환하는 핵분열 & 핵융합 (1) | 2023.10.17 |
|---|---|
| 입자의 위치와 운동량 측정 :: 하이젠베르크의 불확정성 원리 (0) | 2023.10.16 |
| 자연에 존재하는 힘 :: 4가지 기본 힘 (0) | 2023.10.10 |
| 물질의 구성요소 원자와 분자 :: 원자핵(양성자, 중성자), 전자 (0) | 2023.09.07 |
| 섬유의 분류 :: 천연섬유 & 인조섬유 종류 (0) | 2023.09.04 |


